construct

	GΘnΘralitΘs sur les expressions
	Le SystΦme AlgΘbrique (G.A.S.)
	propose une multitude dÆopΘrateurs prΘdΘfinis, dÆopΘrateurs, de fonctions et de constantes. Vue dÆensemble Fonctions gΘomΘtriques OpΘrateurs arithmΘtiques Fonctions arithmΘtiques DΘriver IntΘgrer OpΘrateurs logiques Fonctions logiques Fonctions trigonomΘtriques Autres fonctions Constantes Fonctions gΘomΘtriques Les fonctions gΘomΘtriques requiΦrent des objets comme paramΦtres dÆentrΘe. Le nom de lÆobjet est tout simplement indiquΘ. Pour les objets, dont le nom comporte un indice, celui-ci sera Θcrit avec un `_`. 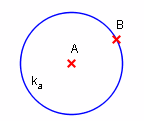Le cercle affichΘ a par exemple le nom `k_a`. Il sera reprΘsentΘ comme `k_a`. Composante x Composante y Distance entre deux points Longueur dÆun segment Rayon dÆun cercle Mesure dÆun angle en degrΘs Mesure dÆun angle en radians Fonction parallΦle Fonction orthogonal Composante x Saisie `X(point)` `point` est un point dans . `X` retourne la valeur de la coordonnΘe x du point. Exemple `X(A)` avec `A(2.23;1.3)` indique `2.23` Composante y Saisie `Y(point)` `point` est un point dans . `Y` retourne la valeur de la coordonnΘe y du point. Exemple `Y(A)` avec `A(2.23;1.3)` indique `1.3` Distance entre deux points Saisie `Dist(point1,point2)` La distance entre les deux point `point1` et `point2` sera calculΘe par `Dist`. Exemple `Dist(A,B)` avec `A(1;0)` et `B(0;1)` retourne `1.414...` Longueur dÆun segment Saisie `L(segment)` `segment` est un segment dans . `L` retourne la longueur du segment en unitΘs de longueur. Si `segment` est une droite, une demi-droite ou un vecteur, la distance entre les deux points de dΘfinition sera retournΘe. Exemple `L(a)` avec `a` dΘfinit par `A(1;0)` et `B(0;1)` indique `1.414...` Rayon dÆun cercle Saisie `R(cercle)` `cercle` est un cercle dans . `R` indique la longueur du rayon dÆun cercle en unitΘs de longueur. Des indices seront dΘcrits par `_` (voir lÆexemple). Exemple `R(k_a)` indique le rayon de `k_a` Mesure dÆangle en degrΘs Saisie `Deg(point1,point2,point3)` `Deg` retourne la mesure de lÆangle `point1` (sur le premier cotΘ) `point2` (Sommet) `point3` (sur le second cotΘ) en degrΘs. Aussi, lÆorientation mathΘmatique de lÆangle est α respecter. Exemple `Deg(A,B,C)` avec `A(1;0)`, `B(0;1)` et `C(1;1)` retourne `45.0` Mesure dÆangle en radians Saisie `Rad(point1,point2,point3)` `Rad` retourne la mesure de lÆangle `point1` (sur le premier cotΘ) `point2` (Sommet) `point3` (sur le second cotΘ) en radians. Exemple `Rad(A,B,C)` avec `A(1;0)`, `B(0;1)` et `C(1;1)` retourne `0.785...` Fonction parallΦle Saisie `Par(droite1, droite 2)` Dans le cas o∙ `droite1` et `droite2` sont parallΦles, la fonction `Par` retourne la valeur `True`, sinon `False`. Exemple `Par(a,b)` avec `a` \|\| `b` donne `True` Fonction orthogonal Saisie `Ortho(droite1, droite2)` Dans le cas o∙ `droite1` et `droite2` sont perpendiculaires, la fonction `Ortho` retourne la valeur `True`, sinon `False`. Exemple `Ortho(a,b)` avec `a` \|\| `b` donne `False` vers le haut OpΘrateurs arithmΘtiques Addition Soustraction Multiplication Division Addition Saisie `argument1 + argument2` Soustraction Saisie `argument1 - argument2` Multiplication Saisie `argument1 * argument2` Division Saisie `argument1 / argument2` vers le haut Fonctions arithmΘtiques Fonction exponentielle Logarithme nΘpΘrien Puissance Racine carrΘe Fonction exponentielle Saisie `Exp(argument)` Exemple `Exp(x)` `Exp(X(A))` Logarithme nΘpΘrien Saisie `Log(argument)` Exemple `Log(x)` `Log(X(A))` `Log(E^2)` donne `2` Puissance Saisies `Pow(base, exposant)` `base^exposant` Exemple `Pow(3, x)` signifie `3^x` `x^2` `Y(C)^2` racine carrΘe Saisie `Sqrt(argument)` Exemple `Sqrt(x)` `Sqrt(Y(B))` vers le haut DΘriver Saisies `D(expression, variable)` `D(expression, {variable, n})` `D(expression, variable)/.variable->valeur` `D(expression, {variable, n})/.variable->valeur` La fonction `D` dΘrive `expression` par rapport α `variable`. `n` indique lÆordre de la dΘrivation et la donnΘe `valeur` sera utilisΘe pour Θvaluer la dΘrivΘe. Exemple `D(Sin(x),x)` donne `Cos(x)` `D(Sin(x),{x,2})` donne `-Sin(x)` `D(Sin(x),x)/.x->Pi/2` donne `0` `D(Sin(x),{x,2})/.x->Pi/2` donne `-1` vers le haut IntΘgrer Saisies `Int(expression, variable)` `Int(expression, variable)/.variable->valeur` La fonction `Int` intΦgre `expression` par rapport α `variable`. La donnΘe `valeur` est utilisΘe pour Θvaluer la primitive. Exemple `Int(Sin(x),x)` donne `-Cos(x)` `Int(Sin(x),x)/.x->Pi` donne `1` vers le haut OpΘrations logiques Θgal supΘrieur supΘrieur ou Θgal infΘrieur infΘrieur ou Θgal diffΘrent OpΘrateur "Θgal" Saisie `argument1 == argument2` OpΘrateur "supΘrieur" Saisie `argument1 > argument2` OpΘrateur "supΘrieur ou Θgal" Saisie `argument1 >= argument2` OpΘrateur "infΘrieur" Saisie `argument1 < argument2` OpΘrateur "infΘrieur ou Θgal" Saisie `argument1 <= argument2` OpΘrateur "diffΘrent" Saisie `argument1 != argument2` vers le haut Fonctions logiques ET logique OU logique Condition ET logique Saisies `And(argument1, ... , argumentN)` `argument1 && ... && argumentN` `And` donne `True`, si tous les arguments sont `True`. Sinon `And` a la valeur `False`. Exemple `And(5>0,3<Pi)` donne `True` `a && b` avec `a=False` et `b=True` donne `False` OU logique Saisies `Or(argument1, ... , argumentN)` `argument1 \|\| ... \|\| argumentN` `Or` donne `True`, si au moins un argument est `True`. Si tous les arguments ont la valeur `False`, alors `Or` donne la valeur `False`. Exemple `Or(5>0,3>Pi)` donne `True` `a \|\| b` avec `a=False` et `b=True` donne `True` Conditions Saisie `If(condition, vrai, faux)` Si `condition` prend la valeur `True`, alors `vrai` est retournΘ, sinon `If` retourne `faux`. Exemple `If(5>0,5.3,4.0)` donne `5.3` `If(5<0,5.3,4.0)` donne `4.0` `If(X(A)<0,X(B)=5,X(B)=X(A))` avec `X(A)=-2.5` donne `X(B)=5` vers le haut Fonctions trigonomΘtriques Arc cosinus Arc sinus Arc tangente Cosinus Cotangente Sinus Tangente Arc cosinus Saisie `ACos(argument)` Exemple `ACos(x)` `ACos(X(A))` Arc sinus Saisie `ASin(argument)` Exemple `ASin(x)` `ASin(X(A))` Arc tangente Saisie `ATan(argument)` Exemple `ATan(x)` `ATan(X(A))` Cosinus Saisie `Cos(argument)` Exemple `Cos(x)` `Cos(X(A))` Cotangente Saisie `Cot(argument)` Exemple `Cot(x)` `Cot(X(A))` Sinus Saisie `Sin(argument)` Exemple `Sin(x)` `Sin(X(A))` Tangente Saisie `Tan(argument)` Exemple `Tan(x)` `Tan(X(A))` vers le haut Autres fonctions Valeur absolue Maximum Minimum Evaluation numΘrique Arrondi Signe Partie entiΦre Valeur absolue Saisie `Abs(argument)` Exemple `Abs(-2)` donne `2` `Abs(x)` donne `-x` pour `x<0`, sinon `x` Maximum Saisie `Max(argument1, ... , argumentN)` Exemple `Max(1,2,3)` donne `3` `Max(-3,0.4,-5.1)` donne `0.4` Minimum Saisie `Min(argument1, ... , argumentN)` Exemple `Min(1,2,3)` donne `1` `Min(-3,0.4,-5.1)` donne `-5.1` Evaluation numΘrique Saisie `N(argument)` Exemple `N(Sqrt(2))` donne `1.414...` `N(E)` donne `2.718...` Arrondi Saisie `Round(argument, n)` La donnΘe `argument` est arrondie α `n` chiffres aprΦs la virgule. Si la valeur arrondie se termine par `0`, ces `0` ne sont pas affichΘs. Si `n` a la valeur `0`, alors le rΘsultat sera affichΘ `.0`. Exemples `Round(2.234623,2)` donne `2.23` `Round(2.234623,3)` donne `2.235` `Round(2.234623,0)` donne `2.0` `Round(2.2300000,4)` donne `2.23` Signe Saisie `Sign(argument)` Exemple `Sign(-2)` donne `-1` `Sign(5.56)` donne `1` `Sign(x)` donne `-1` pour `x<0`, `0` pour `x=0` et `1` pour `x>0` Partie entiΦre Saisie `Trunc(zahl)` Les chiffres aprΦs la virgule sont supprimΘs par la fonction `Trunc`. Le rΘsultat retournΘ est la valeur entiΦre avec `.0`. Exemple `Trunc(3.523453)` donne `3.0` `Trunc(-3.4564564)` donne `-3.0` vers le haut Constantes Nombre Pi Nombre e Faux Vrai Nombre Pi Saisie `Pi` Nombre e Saisie `E` Faux Saisie `Faux` Vrai Saisie `True` vers le haut
	Regardez aussi: Point (x;y) Angle (Donner la mesure) Cercle (Rayon α entrer) Graphe de fonction Courbe paramΘtrΘe Texte

GΘnΘralitΘs sur les expressions